509 斐波那契数
斐波那契数,通常用 F(n) 表示,形成的序列称为斐波那契数列。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给你 n ,请计算 F(n) 。示例 1:
输入:2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1示例 2:
输入:3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2示例 3:
输入:4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3提示:
0 <= n <= 30
递归
class Solution {
public:
int fib(int N) {
if (N < 2) return N;
return fib(N - 1) + fib(N - 2);
}
};- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
动态规划
class Solution {
public:
int fib(int N) {
if (N <= 1) return N;
int dp[2];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= N; i++) {
int sum = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = sum;
}
return dp[1];
}
};- 时间复杂度:O(n)
- 空间复杂度:O(1)
剑指 Offer 25. 合并两个排序的链表
输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。
示例 1:
输入:1->2->4, 1->3->4
输出:1->1->2->3->4->4限制:
0 <= 链表长度 <= 1000
常规题目,类似于归并排序中的合并过程。
递归
/*
*/
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} l1
* @param {ListNode} l2
* @return {ListNode}
*/
var mergeTwoLists = function(l1, l2) {
if (l1 === null) return l2;
if (l2 === null) return l1;
if (l1.val < l2.val) {
l1.next = mergeTwoLists(l1.next, l2);
return l1;
} else {
l2.next = mergeTwoLists(l1, l2.next);
return l2;
}
};- 时间复杂度:O(N),其中 N 为两个链表节点总数
- 空间复杂度:O(1)
迭代
/*
* @lc app=leetcode id=21 lang=javascript
*
*/
/**
* @param {ListNode} l1
* @param {ListNode} l2
* @return {ListNode}
*/
var mergeTwoLists = function(l1, l2) {
let current = new ListNode();
const dummy = current;
while (l1 || l2) {
if (!l1) {
current.next = l2;
return dummy.next;
} else if (!l2) {
current.next = l1;
return dummy.next;
}
if (l1.val <= l2.val) {
current.next = l1;
l1 = l1.next;
} else {
current.next = l2;
l2 = l2.next;
}
current = current.next;
}
return dummy.next;
};- 时间复杂度:O(N),其中 N 为两个链表节点总数
- 空间复杂度:加上栈空间的话,空间复杂度为 O(N),其中 N 为两个链表节点总数
剑指 Offer 24. 反转链表
定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL限制:
0 <= 节点个数 <= 5000
迭代
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var reverseList = function(head) {
let prev = null;
let curr = head;
while (curr) {
const next = curr.next; // 修改前先记住下一个节点
curr.next = prev; // 改指向,第一个节点 prev 是 null
prev = curr; // 记录前一个节点,供下次循环使用
curr = next; // curr 通过 next 指向下一节点
}
return prev; // curr 会循环直到 null
};- 时间复杂度:O(n),其中 n 是链表的长度。需要遍历链表一次。
- 空间复杂度:O(1)。
递归
var reverseList = function(head) {
if (head == null || head.next == null) {
return head;
}
const newHead = reverseList(head.next);
// 放在递归函数的后面是为了倒序遍历
// 假设节点 n(k + 1) 到 n(m) 已经反转
// 希望 n(k + 1) 的下一个节点指向 n(k),所以 n(k).next.next = n(k)
head.next.next = head;
head.next = null; // 避免产生环
return newHead;
};- 时间复杂度:O(n),其中 n 是链表的长度。需要对链表的每个节点进行反转操作。
- 空间复杂度:O(n),其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间,最多为 n 层。
141. 环形链表
给定一个链表,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true。否则,返回 false。
进阶:
你能用 O(1)(即,常量)内存解决此问题吗?
示例 1:
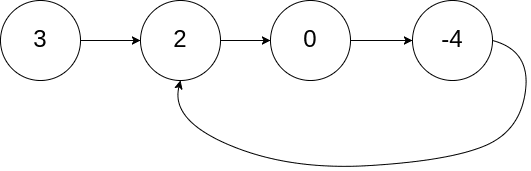
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。示例 2:
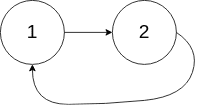
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。示例 3:

输入:head = [1], pos = -1
输出:false
解释:链表中没有环。提示:
- 链表中节点的数目范围是 [0, 104]
- -105 <= Node.val <= 105
- pos 为 -1 或者链表中的一个有效索引。
哈希表
class Solution {
public:
bool hasCycle(ListNode *head) {
unordered_set<ListNode*> seen;
while (head != nullptr) {
if (seen.count(head)) {
return true;
}
seen.insert(head);
head = head->next;
}
return false;
}
};- 时间复杂度:O(N),其中 N 是链表中的节点数。最坏情况下我们需要遍历每个节点一次。
- 空间复杂度:O(N),其中 N 是链表中的节点数。主要为哈希表的开销,最坏情况下我们需要将每个节点插入到哈希表中一次。
快慢指针
class Solution {
public:
bool hasCycle(ListNode* head) {
if (head == nullptr || head->next == nullptr) {
return false;
}
ListNode* slow = head;
ListNode* fast = head->next;
while (slow != fast) {
if (fast == nullptr || fast->next == nullptr) {
return false;
}
slow = slow->next;
fast = fast->next->next;
}
return true;
}
};-
时间复杂度:O(N),其中 N 是链表中的节点数。
- 当链表中不存在环时,快指针将先于慢指针到达链表尾部,链表中每个节点至多被访问两次。
- 当链表中存在环时,每一轮移动后,快慢指针的距离将减小一。而初始距离为环的长度,因此至多移动 N 轮。
- 空间复杂度:O(1)。我们只使用了两个指针的额外空间。
678. 有效的括号字符串
给定一个只包含三种字符的字符串:( ,) 和 *,写一个函数来检验这个字符串是否为有效字符串。有效字符串具有如下规则:
- 任何左括号 ( 必须有相应的右括号 )。
- 任何右括号 ) 必须有相应的左括号 ( 。
- 左括号 ( 必须在对应的右括号之前 )。
- * 可以被视为单个右括号 ) ,或单个左括号 ( ,或一个空字符串。
- 一个空字符串也被视为有效字符串。
示例 1:
输入: "()"
输出: True示例 2:
输入: "(*)"
输出: True示例 3:
输入: "(*))"
输出: True注意:
- 字符串大小将在
[1,100]范围内。
栈
两个栈, 一个存放( ,一个存放 * 栈中存放下标
var checkValidString = function(s) {
let stack = [],
star = [];
for (let i = 0; i < s.length; i++) {
// 一遍遍历,对每一个 s[i],判断是入栈还是抵消
if (s[i] == '(') stack.push(i);
else if (s[i] == '*') star.push(i);
else {
if (stack.length) stack.pop();
else if (star.length) star.pop();
else return false; // 没得抵消了,只能返回 false
}
}
if (stack.length > star.length) return false; // 对两个栈处理
while (stack.length && star.length) {
if (stack.pop() > star.pop()) return false; // **((, 类似这样,虽个数合适,但顺序(下标)不可
}
return true;
};贪心
我们只需要维护一个左括号的可能取值数组即可
- 当我们遇到(的时候,我们的左括号的数量区间就是
[1],只能是一个。 -
当我们遇到(*的时候,我们的左括号的数量区间是
[0,1,2],- 星号可以当成右括号,这样就会和前面一个左括号抵消,相当于没有括号,是为 0;
- 星号可以当成空字符串,那就是 1;
- 如果当成左括号,那就是 2;
- 如果我们遇到星号之前的区间是
[0,1],那这里是不是变成了[-1,0,1,2]了呢?没有必要,因为我们要尽可能的平衡左右括号,所以显然不能愣头青地强行要把星号当成)来使左括号取值变成-1,所以是[0,1,2]
- 当我们遇到)的时候,我们的区间取值是否都要降低 1,比如
[0,1,2]变成[-1,0,1]呢?这里需要注意,我们是要尽可能的平衡左右括号,所以当我们的区间最左值已经是 0 的时候,我们显然要把之前的星号当成(来抵消这个),跟上面那个类似,都是贪心思想的体现。所以我们这里只需要把区间改成[0,1]
最后我们遍历完字符串以后,我们只需要检查我们的区间是不是包含了 0,因为这个区间是连续的,所以我们只需要判断最左侧的值和最后侧的值是否夹住了 0,即 low<=0&&0<=high
/**
* @param {string} s
* @return {boolean}
*/
var checkValidString = function(s) {
let low = 0;
let high = 0;
for (let i = 0; i < s.length; i++) {
if (s[i] == '(') {
low++;
high++;
} else if (s[i] == ')') {
// 贪心缩小区间
if (low > 0) --low;
if (high > 0) {
--high;
} else {
return false;
}
} else {
// 贪心缩小区间
if (low > 0) {
low--;
}
high++;
}
}
return low <= 0 && 0 <= high;
};215. 数组中的第 K 个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4提示:
- 1 <= k <= nums.length <= 104
- -104 <=
nums[i]<= 104
数组排序
let findKthLargest = function(nums, k) {
nums.sort((a, b) => b - a).slice(0, k);
return nums[k - 1];
};- 时间复杂度:O(nlogn)
- 空间复杂度:O(logn)
构造前 k 个最大元素小顶堆,取堆顶
通过构造一个前 k 个最大元素小顶堆来解决,小顶堆上的任意节点值都必须小于等于其左右子节点值,即堆顶是最小值。
所以我们可以从数组中取出 k 个元素构造一个小顶堆,然后将其余元素与小顶堆对比,如果大于堆顶则替换堆顶,然后堆化,所有元素遍历完成后,堆中的堆顶即为第 k 个最大值
具体步骤如下:
- 从数组中取前 k 个数( 0 到 k-1 位),构造一个小顶堆
- 从 k 位开始遍历数组,每一个数据都和小顶堆的堆顶元素进行比较,如果小于堆顶元素,则不做任何处理,继续遍历下一元素;如果大于堆顶元素,则将这个元素替换掉堆顶元素,然后再堆化成一个小顶堆。
- 遍历完成后,堆顶的数据就是第 K 大的数据
let findKthLargest = function(nums, k) {
// 从 nums 中取出前 k 个数,构建一个小顶堆
let heap = [,],
i = 0;
while (i < k) {
heap.push(nums[i++]);
}
buildHeap(heap, k);
// 从 k 位开始遍历数组
for (let i = k; i < nums.length; i++) {
if (heap[1] < nums[i]) {
// 替换并堆化
heap[1] = nums[i];
heapify(heap, k, 1);
}
}
// 返回堆顶元素
return heap[1];
};
// 原地建堆,从后往前,自上而下式建小顶堆
let buildHeap = (arr, k) => {
if (k === 1) return;
// 从最后一个非叶子节点开始,自上而下式堆化
for (let i = Math.floor(k / 2); i >= 1; i--) {
heapify(arr, k, i);
}
};
// 堆化
let heapify = (arr, k, i) => {
// 自上而下式堆化
while (true) {
let minIndex = i;
if (2 * i <= k && arr[2 * i] < arr[i]) {
minIndex = 2 * i;
}
if (2 * i + 1 <= k && arr[2 * i + 1] < arr[minIndex]) {
minIndex = 2 * i + 1;
}
if (minIndex !== i) {
swap(arr, i, minIndex);
i = minIndex;
} else {
break;
}
}
};
// 交换
let swap = (arr, i, j) => {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
};- 时间复杂度:遍历数组需要 O(n) 的时间复杂度,一次堆化需要 O(logk) 时间复杂度,所以利用堆求 Top k 问题的时间复杂度为 O(nlogk)
- 空间复杂度:O(k)
快速选择(quickselect)算法
let findKthLargest = function(nums, k) {
return quickSelect(nums, nums.length - k);
};
let quickSelect = (arr, k) => {
return quick(arr, 0, arr.length - 1, k);
};
let quick = (arr, left, right, k) => {
let index;
if (left < right) {
// 划分数组
index = partition(arr, left, right);
// Top k
if (k === index) {
return arr[index];
} else if (k < index) {
// Top k 在左边
return quick(arr, left, index - 1, k);
} else {
// Top k 在右边
return quick(arr, index + 1, right, k);
}
}
return arr[left];
};
let partition = (arr, left, right) => {
// 取中间项为基准
var datum = arr[Math.floor(Math.random() * (right - left + 1)) + left],
i = left,
j = right;
// 开始调整
while (i < j) {
// 左指针右移
while (arr[i] < datum) {
i++;
}
// 右指针左移
while (arr[j] > datum) {
j--;
}
// 交换
if (i < j) swap(arr, i, j);
// 当数组中存在重复数据时,即都为 datum,但位置不同
// 继续递增 i,防止死循环
if (arr[i] === arr[j] && i !== j) {
i++;
}
}
return i;
};
// 交换
let swap = (arr, i, j) => {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
};- 时间复杂度:平均时间复杂度 O(n),最坏情况时间复杂度为 O(n^2)
- 空间复杂度:O(1)
中位数的中位数(BFPRT)算法
又称为中位数的中位数算法,它的最坏时间复杂度为 O(n),它是由 Blum、Floyd、Pratt、Rivest、Tarjan 提出。该算法的思想是修改快速选择算法的主元选取方法,提高算法在最坏情况下的时间复杂度。
在 BFPTR 算法中,仅仅是改变了快速选择(quickselect)算法中 Partion 中的基准值的选取,在快速选择(quickselect)算法中,我们可以选择第一个元素或者最后一个元素作为基准元,优化的可以选择随机一个元素作为基准元,而在 BFPTR 算法中,每次选择五分中位数的中位数作为基准元(也称为主元 pivot),这样做的目的就是使得划分比较合理,从而避免了最坏情况的发生。
BFPRT 算法步骤如下:
-
选取主元
- 将 n 个元素按顺序分为 n/5 个组,每组 5 个元素,若有剩余,舍去
- 对于这 n/5 个组中的每一组使用插入排序找到它们各自的中位数
- 对于上一步中找到的所有中位数,调用 BFPRT 算法求出它们的中位数,作为主元;
- 以主元为分界点,把小于主元的放在左边,大于主元的放在右边;
- 判断主元的位置与 k 的大小,有选择的对左边或右边递归
let findKthLargest = function(nums, k) {
return nums[bfprt(nums, 0, nums.length - 1, nums.length - k)];
};
let bfprt = (arr, left, right, k) => {
let index;
if (left < right) {
// 划分数组
index = partition(arr, left, right);
// Top k
if (k === index) {
return index;
} else if (k < index) {
// Top k 在左边
return bfprt(arr, left, index - 1, k);
} else {
// Top k 在右边
return bfprt(arr, index + 1, right, k);
}
}
return left;
};
let partition = (arr, left, right) => {
// 基准
var datum = arr[findMid(arr, left, right)],
i = left,
j = right;
// 开始调整
while (i < j) {
// 左指针右移
while (arr[i] < datum) {
i++;
}
// 右指针左移
while (arr[j] > datum) {
j--;
}
// 交换
if (i < j) swap(arr, i, j);
// 当数组中存在重复数据时,即都为datum,但位置不同
// 继续递增i,防止死循环
if (arr[i] === arr[j] && i !== j) {
i++;
}
}
return i;
};
/**
* 数组 arr[left, right] 每五个元素作为一组,并计算每组的中位数,
* 最后返回这些中位数的中位数下标(即主元下标)。
*
* @attention 末尾返回语句最后一个参数多加一个 1 的作用其实就是向上取整的意思,
* 这样可以始终保持 k 大于 0。
*/
let findMid = (arr, left, right) => {
if (right - left < 5) return insertSort(arr, left, right);
let n = left - 1;
// 每五个作为一组,求出中位数,并把这些中位数全部依次移动到数组左边
for (let i = left; i + 4 <= right; i += 5) {
let index = insertSort(arr, i, i + 4);
swap(arr[++n], arr[index]);
}
// 利用 bfprt 得到这些中位数的中位数下标(即主元下标)
return findMid(arr, left, n);
};
/**
* 对数组 arr[left, right] 进行插入排序,并返回 [left, right]
* 的中位数。
*/
let insertSort = (arr, left, right) => {
let temp, j;
for (let i = left + 1; i <= right; i++) {
temp = arr[i];
j = i - 1;
while (j >= left && arr[j] > temp) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = temp;
}
return ((right - left) >> 1) + left;
};
// 交换
let swap = (arr, i, j) => {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
};- 时间复杂度:最坏 O(n)
- 空间复杂度:O(1)
寻找和为定值的多个数
输入两个整数 n 和 sum,从数列 1,2,3…n 中随意取几个数,使其和等于 sum,要求将其中所有的可能组合列出来。
递归
注意到取 n,和不取 n 个区别即可,考虑是否取第 n 个数的策略,可以转化为一个只和前 n-1 个数相关的问题。
- 如果取第 n 个数,那么问题就转化为“取前 n-1 个数使得它们的和为 sum-n”,对应的代码语句就是 sumOfkNumber(sum - n, n - 1);
- 如果不取第 n 个数,那么问题就转化为“取前 n-1 个数使得他们的和为 sum”,对应的代码语句为 sumOfkNumber(sum, n - 1)。
list<int>list1;
void SumOfkNumber(int sum, int n)
{
// 递归出口
if (n <= 0 || sum <= 0)
return;
// 输出找到的结果
if (sum == n)
{
// 反转 list
list1.reverse();
for (list<int>::iterator iter = list1.begin(); iter != list1.end(); iter++)
cout << *iter << " + ";
cout << n << endl;
list1.reverse() // 此处还需反转回来
}
list1.push_front(n); // 典型的 01 背包问题
SumOfkNumber(sum - n, n - 1); // “放” n,前 n-1 个数“填满” sum-n
list1.pop_front();
SumOfkNumber(sum, n - 1); // 不“放” n,n-1 个数“填满” sum
}回溯法+剪枝
这个问题属于子集和问题(也是背包问题)。本程序采用回溯法+剪枝,其中 X 数组是解向量,t=∑(1,..,k-1)Wi*Xi, r=∑(k,..,n)Wi,且
若 t+Wk+W(k+1)<=M,则 Xk=true,递归左儿子(X1,X2,..,X(k-1),1);否则剪枝;若 t+r-Wk>=M && t+W(k+1)<=M,则置 Xk=0,递归右儿子(X1,X2,..,X(k-1),0);否则剪枝;本题中 W 数组就是(1,2,..,n),所以直接用 k 代替 WK 值。
//输入t, r,尝试 Wk
void SumOfkNumber(int t, int k, int r, int& M, bool& flag, bool* X)
{
X[k] = true; // 选第 k 个数
if (t + k == M) // 若找到一个和为 M,则设置解向量的标志位,输出解
{
flag = true;
for (int i = 1; i <= k; ++i)
{
if (X[i] == 1)
{
printf("%d ", i);
}
}
printf("\n");
}
else
{ // 若第 k+1 个数满足条件,则递归左子树
if (t + k + (k + 1) <= M)
{
SumOfkNumber(t + k, k + 1, r - k, M, flag, X);
}
// 若不选第 k 个数,选第 k+1 个数满足条件,则递归右子树
if ((t + r - k >= M) && (t + (k + 1) <= M))
{
X[k] = false;
SumOfkNumber(t, k + 1, r - k, M, flag, X);
}
}
}
void search(int& N, int& M)
{
// 初始化解空间
bool* X = (bool*)malloc(sizeof(bool)* (N + 1));
memset(X, false, sizeof(bool)* (N + 1));
int sum = (N + 1) * N * 0.5f;
if (1 > M || sum < M) // 预先排除无解情况
{
printf("not found\n");
return;
}
bool f = false;
SumOfkNumber(0, 1, sum, M, f, X);
if (!f)
{
printf("not found\n");
}
free(X);
}0-1 背包问题
0-1 背包问题是最基础的背包问题,其具体描述为:有 N 件物品和一个容量为 V 的背包。放入第 i 件物品耗费的费用是 Ci,得到的价值是 Wi。求解将哪些物品装入背包可使价值总和最大。
简单分析下:这是最基础的背包问题,特点是每种物品仅有一件,可以选择放或不放。用子问题定义状态:即 F[i, v]表示前 i 件物品恰放入一个容量为 v 的背包可以获得的最大价值。则其状态转移方程便是:
F[i, v] = max{F[i-1, v], F[i-1, v-Ci] + Wi} 根据前面的分析,我们不难理解这个方程的意义:“将前 i 件物品放入容量为 v 的背包中”这个子问题,若只考虑第 i 件物品的策略(放或不放),那么就可以转化为一个只和前 i-1 件物品相关的问题。即:
如果不放第 i 件物品,那么问题就转化为“前 i-1 件物品放入容量为 v 的背包中”,价值为 F[i-1, v ];如果放第 i 件物品,那么问题就转化为“前 i-1 件物品放入剩下的容量为 v-Ci 的背包中”,此时能获得的最大价值就是 F[i-1, v-Ci]再加上通过放入第 i 件物品获得的价值 Wi。
F[0,0...V] ← 0
for i ← 1 to N
for v ← Ci to V
F[i, v] ← max{F[i-1, v], F[i-1, v-Ci] + Wi }这段代码的时间和空间复杂度均为 O(VN),其中时间复杂度应该已经不能再优化了,但空间复杂度却可以优化到 O(V)。
1663. 具有给定数值的最小字符串
小写字符的数值是它在字母表中的位置(从 1 开始),因此 a 的数值为 1,b 的数值为 2,c 的数值为 3,以此类推。
字符串由若干小写字符组成,字符串的数值为各字符的数值之和。例如,字符串 “abe” 的数值等于 1 + 2 + 5 = 8。
给你两个整数 n 和 k。返回长度等于 n 且数值等于 k 的字典序最小的字符串。
注意,如果字符串 x 在字典排序中位于 y 之前,就认为 x 字典序比 y 小,有以下两种情况:
- x 是 y 的一个前缀;
- 如果 i 是
x[i] != y[i]的第一个位置,且x[i]在字母表中的位置比y[i]靠前。
示例 1:
输入:n = 3, k = 27
输出:"aay"
解释:字符串的数值为 1 + 1 + 25 = 27,它是数值满足要求且长度等于 3 字典序最小的字符串。示例 2:
输入:n = 5, k = 73
输出:"aaszz"提示:
- 1 <= n <= 10^5
- n <= k <= 26 * n
构造不等式
利用 k 和 n 之间的关系构造不等式,从而取到每一位上的最小值
/**
* @param {number} n
* @param {number} k
* @return {string}
*/
var getSmallestString = function(n, k) {
var len = n;
var res = [];
var charA = 'a'.charCodeAt(0);
for (var i = 0; i < n; i++) {
var bound = k - (n - 1 - i) * 26;
if (bound <= 1) {
res[i] = 'a';
k -= 1;
} else {
res[i] = String.fromCharCode(charA + bound - 1);
k -= bound;
}
}
res = res.join('');
return res;
};全部填充 a,再从后往前消耗 k
var getSmallestString = function(n, k) {
var res = [];
for (var i = 0; i < n; i++) {
res.push('a');
}
var remain = k - n;
var current = n - 1;
while (remain > 0) {
if (remain > 25) {
res[current] = 'z';
remain -= 25; // 前面已经减过 1 了
current -= 1;
} else {
res[current] = String.fromCharCode(97 + remain);
remain = 0;
}
}
return res.join('');
};剑指 Offer 55 - I. 二叉树的深度
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。
例如:
给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7返回它的最大深度 3 。
提示:
- 节点总数 <= 10000
深度优先(递归)
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
const maxDepth = (root) => {
// 1. 如果没下一层了,返回 0
if (!root) {
return 0;
}
// 2. 返回左右子树中最深的那一层
return Math.max(maxDepth(root.left) + 1, maxDepth(root.right) + 1);
};
const root = {
val: 3,
left: { val: 9 },
right: {
val: 20,
left: { val: 15, left: null, right: null },
right: { val: 7, left: null, right: null }
}
};
console.log(maxDepth(root));广度优先
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
const maxDepth = (root) => {
if (!root) {
return 0;
}
// 1. 设置深度为 0
let depth = 0;
// 2. 每层遍历
let bfs = [root];
// 3. 逐层访问树
while (bfs.length) {
// 3.1 每次遍历,深度 + 1
depth++;
// 3.2 设置下一次需要遍历的节点
const tempBfs = [];
// 3.3 遍历本次所有节点,将有内容的都添加进来
for (let i = 0; i < bfs.length; i++) {
if (bfs[i].left) {
tempBfs.push(bfs[i].left);
}
if (bfs[i].right) {
tempBfs.push(bfs[i].right);
}
}
// 3.4 交接 tempBfs 到 bfs 上
bfs = tempBfs;
}
// 4. 返回深度
return depth;
};
const root = {
val: 3,
left: { val: 9 },
right: {
val: 20,
left: { val: 15, left: null, right: null },
right: { val: 7, left: null, right: null }
}
};102. 二叉树的层序遍历
给你一个二叉树,请你返回其按层序遍历得到的节点值。(即逐层地,从左到右访问所有节点)。
示例:
二叉树:[3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7返回其层序遍历结果:
[
[3],
[9,20],
[15,7]
]广度优先搜索
var levelOrder = function(root) {
const ret = [];
if (!root) {
return ret;
}
const q = [];
q.push(root);
while (q.length !== 0) {
const currentLevelSize = q.length;
ret.push([]);
for (let i = 1; i <= currentLevelSize; ++i) {
const node = q.shift();
ret[ret.length - 1].push(node.val);
if (node.left) q.push(node.left);
if (node.right) q.push(node.right);
}
}
return ret;
};- 时间复杂度:每个点进队出队各一次,故渐进时间复杂度为 O(n)。
- 空间复杂度:队列中元素的个数不超过 n 个,故渐进空间复杂度为 O(n)。
36. 有效的数独
请你判断一个 9x9 的数独是否有效。只需要根据以下规则,验证已经填入的数字是否有效即可。
- 数字 1-9 在每一行只能出现一次。
- 数字 1-9 在每一列只能出现一次。
- 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ’.’ 表示。
注意:
- 一个有效的数独(部分已被填充)不一定是可解的。
- 只需要根据以上规则,验证已经填入的数字是否有效即可。
示例 1:

输入:board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出:true示例 2:
输入:board =
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出:false
解释:除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。迭代
class Solution {
public:
bool isValidSudoku(vector<vector<char>>& board) {
vector<vector<int>> row (9, vector<int>(9,0));
vector<vector<int>> col (9, vector<int>(9,0));
vector<vector<int>> box (9, vector<int>(9,0));
for(int i=0;i<9;i++) {
for(int j=0;j<9;j++) {
if(board[i][j] == '.') {
continue;
}
int val = board[i][j] - '1';
int box_index = (i/3) * 3 + j/3;
if(row[i][val] == 0 && col[j][val] == 0 && box[box_index][val] == 0) {
row[i][val] = 1;
col[j][val] = 1;
box[box_index][val] = 1;
}
else {
return false;
}
}
}
return true;
}
};69. x 的平方根
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:
输入: 4
输出: 2示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。袖珍计算器算法
class Solution {
public:
int mySqrt(int x) {
if (x == 0) {
return 0;
}
int ans = exp(0.5 * log(x));
return ((long long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans);
}
};- 时间复杂度:O(1),由于内置的 exp 函数与 log 函数一般都很快,我们在这里将其复杂度视为 O(1)。
- 空间复杂度:O(1)。
二分查找
class Solution {
public:
int mySqrt(int x) {
int l = 0, r = x, ans = -1;
while (l <= r) {
int mid = l + (r - l) / 2;
if ((long long)mid * mid <= x) {
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return ans;
}
};- 时间复杂度:O(logx),即为二分查找需要的次数。
- 空间复杂度:O(1)。
牛顿迭代
class Solution {
public:
int mySqrt(int x) {
if (x == 0) {
return 0;
}
double C = x, x0 = x;
while (true) {
double xi = 0.5 * (x0 + C / x0);
if (fabs(x0 - xi) < 1e-7) {
break;
}
x0 = xi;
}
return int(x0);
}
};- 时间复杂度:O(logx),此方法是二次收敛的,相较于二分查找更快。
- 空间复杂度:O(1)。
208. 实现 Trie (前缀树)
Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
- Trie() 初始化前缀树对象。
- void insert(String word) 向前缀树中插入字符串 word 。
- boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false。
- boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix,返回 true;否则,返回 false。
示例:
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]
解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True提示:
- 1 <= word.length, prefix.length <= 2000
- word 和 prefix 仅由小写英文字母组成
- insert、search 和 startsWith 调用次数总计不超过 3 * 104 次
字典树
var Trie = function() {
this.children = {};
};
Trie.prototype.insert = function(word) {
let node = this.children;
for (const ch of word) {
if (!node[ch]) {
node[ch] = {};
}
node = node[ch];
}
node.isEnd = true;
};
Trie.prototype.searchPrefix = function(prefix) {
let node = this.children;
for (const ch of prefix) {
if (!node[ch]) {
return false;
}
node = node[ch];
}
return node;
};
Trie.prototype.search = function(word) {
const node = this.searchPrefix(word);
return node !== undefined && node.isEnd !== undefined;
};
Trie.prototype.startsWith = function(prefix) {
return this.searchPrefix(prefix);
};- 时间复杂度:初始化为 O(1),其余操作为 O(|S|),其中 |S| 是每次插入或查询的字符串的长度。
- 空间复杂度:O(|T|⋅Σ),其中 |T| 为所有插入字符串的长度之和,Σ 为字符集的大小,本题 Σ=26。